1. Sayı - Akıl Oyunları Cevapları
1. Kibritlerden Şekiller
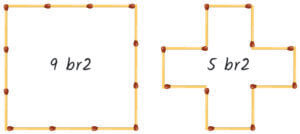
Kibrit bir uzunluk birimi olarak düşünüldüğünde, onunla birbirinden farklı geometrik şekiller oluşturulabilir.
Yukarıdaki resimde 12 kibrit ile oluşturulan iki farklı şekil ve bu şekillerin alanları gösterilmiştir.
Bu 12 kibriti kırmadan ve tamamını kullanarak alanı 4 birim kare olan bir geometrik şekil oluşturabilir misiniz?
Şekli oluşturduktan sonra alan hesabını da yapmalısınız.
Yanıt
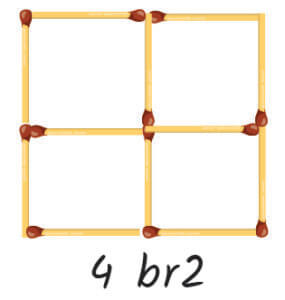
Sizler için tüm kibritleri kullanarak alanı 4 birim kare olan bir şekil oluşturduk. Siz de farklı yanıtlar bulabilirsiniz.
2. Bayan Tardogi Kaç Yaşında?
Obix gezegeninde zaman Bort-2 gezegeninde olduğundan 3 kat hızlı geçmektedir.
Obix gezegeninde yaşayan Bay Kraptulos ve Bayan Tardogi isimli iki uzaylı aynı yaştadır.
Bayan Tardogi bir gün ışık hızına yakın hızda hareket eden bir uzay mekiğiyle Bort-2 gezegenine seyahat eder.
Bay Kraptulos Obix gezegeninde 12 yıl boyunca Bayan Tardogi’den ayrı yaşar. Sonra bir gün Bayan Tardogi aynı uzay mekiğiyle tekrar Obix gezegenine döner. Döndüğünde Bay Kraptulos ile Bayan Tardogi’nin yaşları toplamı 76 olduğuna göre, Bayan Tardogi Obix gezegeninden ayrılmadan önce kaç yaşındadır?
Yanıt
Bayan Tardogi, Bort-2 gezegenine seyahat ettikten sonra, Bay Kraptulos’un gezegeni olan Obix’te zaman, Bayan Tardogi’ye göre 3 kat hızlı geçmeye başlar.
Bu yüzden Bay Kraptulos’a göre Obix gezegeninde 12 yıl geçtiğinde, Bayan Tardogi’nin gezegeni olan Bort-2’de sadece 4 yıl geçmiştir.
Bayan Tardogi Obix’e geri dödüğünde 4 yaş yaşlanmıştır. Bay Tardogi ise 12 yaş yaşlanmıştır.
Başlangıçta aynı yaşta olduklarına göre, ikisinin aradan geçen zaman boyunca aldıkları yaşların toplamını şu anki yaşları toplamından çıkararak, başlangıçtaki yaşları toplamını 60 olarak buluruz.
Başlangıçta aynı yaşta olduklarına göre ikisinin de yaşı 30’dur.
3. Dünyayı Saran İp
Ekvator üzerinde dünyayı çevreleyen ve zemin üzerinde duran bir ip olduğunu düşünün.
Bu ipi tüm ekvator boyunca 2 metre bollaştırarak her bulunduğu yüzeyden 2 metre yüksekte durması isteniyor.
Bunun için kaç metre daha ip eklemek gerekir?
Yanıt
Dünyanın çevresi ekvator çizgisi boyunca yaklaşık 40.030 km’dir.
Dünyanın çapı 12.742 km’dir.
Ekvator çizgisini bir çember olarak farz edersek, çevresini hesaplamak için kullanmamız gereken formül aşağıdaki gibi olur.
2.π.r = 2.π.6371 = 40030
Bu formülde “π” Pi sayısını, “r” ise dünyanın yarıçapı yerine kullanılır.
Dünya yüzeyini saran ip her yüzeyden 2m uzakta duracak şekilde bollaştırılırsa, bu ipin başlangıçta 12.742 km olan çapı 4 km daha fazla olacaktır.
Bu durumda dünyanın yarıçapı olan r de 6373 km olacaktır.
Bu durumda bu ipin yeni çapı yaklaşık olarak aşağıdaki gibi hesaplanır.
2.π.r = 2.π.6373 = 40043 km
4. Renkli Küpler
Alis Harikalar Diyarında kitabının yazarı Lewis Carroll’un eski matematik öğretmeni Profesör Bartholomew Price’a gönderdiği çalışmalar arasında bir soru yer alır.
Elinizde ahşap küpler olduğunu varsayalım.
Ayrıca hepsi farklı renkte altı boya kutunuz var.
Bir küpün altı yüzünü hep farklı renklerle boyuyorsunuz.
Bu altı boya kutusu ile kaç farklı küp boyayabilirsiniz?
Bir küpün diğerinden farklı olması için, küpleri ne şekilde tutarsanız tutun renk
sıralamasının aynı olmaması gerekir.
Yanıt
6 kutu farklı boya ile otuz farklı küp boyanabilir.
Küpün altı yüzüne a, b, c, d, e ve f diyelim. a’nın karşısındaki yüze b dersek, diğer yüzler küpün etrafında altı farklı şekilde yerleştirilebilir.
cdef, cdfe, cedf, cefd, cfde ve cged.
Benzer şekilde a’nın karşısındaki yüze sırasıyla c, d, e ve f dersek hepsi diğer dört renk için altışar seçenek yaratır. Dolayısıyla farklı renk düzenlemesine sahip küp sayısı 5×6=30 olur.
5. Sarı, Siyah ve Kırmızı
‘Sarı’ takma adıyla tanınan bir fizikçi, ‘siyah’ takma adlı bir matematikçi ve ‘kırmızı’ takma adlı bir tarihçi dışarıda buluşurlar.
İçlerinden birisi: “Benim saçım siyah, birinizinki kırmızı, diğerinizinki de sarı, ama hiçbirimizin takma adıyla saç rengi birbirini tutmuyor.” der. Sarı, “Çok haklısın” diye yanıtlar.
Buna göre tarihçinin saç rengi nedir?
Yanıt
İlk kişi kendi saçının siyah olduğunu söylüyor. Aynı zamanda hiçbirinin saç rengiyle takma adının aynı olmadığını söylüyor.
İkinci kişi olan Sarı takma adlı kişi de bu durumu doğruluyor.
Bu durumda ilk kişinin saçının rengi siyahtır, takma adı da Siyah olamayacağı için ya Kırmızı ya da Sarı’dır. İkinci konuşan kişinin takma adı Sarı olduğundan birinci kişinin takma adı da kesinlikle Kırmızı’dır.
İkinci kişinin takma adı Sarı’dır. Saç rengi takma adıyla aynı olamayacağından ya siyah ya da kırmızı olmalıdır. İlk kişinin saç rengi siyah olduğundan, Sarı’nın saç rengi kesinlikle kırmızıdır.
Bu durumda üçüncü kişinin takma adı da Siyah’tır ve saç rengi de kesinlikle sarıdır.
Özetleyecek olursak:
Kırmızı’nın saç rengi siyahtır.
Sarı’nın saç rengi kırmızıdır.
Siyah’ın saç rengi sarıdır.
Bu durumda Kırmızı takma adıyla anılan tarihçinin saç rengi siyahtır.
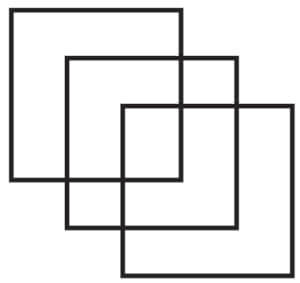
6. İç İçe Kareler
Aşağıdaki iç içe geçmiş üç kareyi kaleminizi hiç kaldırmadan, bir çizginin üzerinden ikinci kez geçmeden ve çizgileri kesiştirmeden çizebilir misiniz?